Hi,
If you have 3 isolated Positions in an argument map, say A, B, and C from Left to Right, can you override FLs automatic positioning?
So if the current positions are
A B C
, is there a way to change the order into
B C A
, so that A is on the right?
Not permanently, no. The automatic layout is what differentiates Flying Logic from a diagramming tool like Visio.
Check out Incremental Layout, which is mentioned in the Quick Start Video at 20:55, and here in the documentation.
Thanks, I know about the Incremental option, but I don’t want to activate it at this point in the map. It’s about 60 percent complete.
Can you recommend a procedural option? In other words, instead of 3 separate positions, it becomes 2 positions, and C can be construed in some other way?
The type of Positions I’m working with in this group, are 2 positions A) and B) that are normally considered binary dichotomies. C is an alternative or list of alternatives. In my project, C) is auto-located to the left.
So A and B might be something like
A = Coke
B = Pepsi
C = All other sodas or no soda or soft drink at all.
A = Vote Democrat
B = Vote Republican
C = Don’t vote, or vote independent or vote Third Party or Vote Dem this year, Third Party next year or vote Independent.
In all these cases, it makes more sense that C is visually to the right - or is some other type of entity.
In a graph, each node (entity) has a set of “predecessors” (entities with arrows to this entity) and a set of “successors” (entities with arrows from this entity). Let’s consider an entity A and it’s predecessors, B, C, and D:
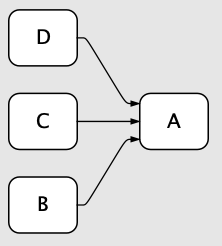
Notice that above I said “set of predecessors.” In mathematics, the elements of a set are unordered. Of course, to lay out A’s predecessors on a two-dimensional canvas, we have to put them in some order, and this is determined by the layout engine.
So why can’t you just, say, reorder them as “B C D” from top to bottom? Several reasons.
First, imposing a specific order on siblings would add semantic information to the ordering. Then, rather than simply reading the diagram as it is drawn, any set of predecessors or successors would then have to be read as possibly having meaning to their order. This breaks the simple idea that only marks on the canvas have meaning— marks like entities, the edges between them, and groups— and introduces the idea that the order of marks might have meaning; a possible source of ambiguity and confusion. If you need to imply order, you can often do so by giving your entities titles that suggest the order like “1. Red”, “2. Green”, “3. Blue”.
Secondly and more importantly, trying to hold an imposed order constant as you modify the document would severely limit the ability of the layout engine to do its job, and would frequently lead to unsolvable situations. So let’s say I group B and A:
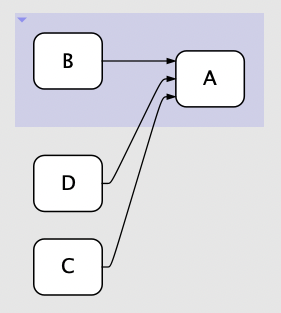
The visual order of B, C, and D has now changed. Let’s say I now move C into the group:
The order has changed again. Now let’s say I insert an entity on the edge D → A:
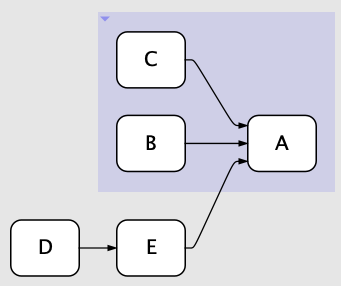
What order are B, C, and D in now? How could we even preserve a specific imposed ordering among them?
Flying Logic is based on the idea that specific drawn objects the relationships between them are all that matters. The layout order of those objects on the canvas specifically does not and cannot carry meaning. As the planner, you focus on creating models and relationships between them using Flying Logic’s four elements: entities, edges, junctors, and groups, and Flying Logic takes care of the rest.
Thanks W.M.,
Yes, I understand the point about Order being irrelevant between Positions ; and that I unwittingly was trying to sneak in some semantic elements.
I think the answer to the follow-up question, about what else can we do about C, is that it should be part of a conditional, or maybe it should be considered a But/However. It’s not really the same type of animal as A or B.
I’ll think about this more, thanks.